Evaluating Azure ML Regression Results.

In the earlier article, we used Azure ML Designer to build a regression model. The final output of the regression model is few metrics which we use to understand how good our regression model is.

There are two steps of interest in evaluating the efficiency of the model. The score model step predicts the price, and evaluate model step finds the difference between prediction and actual price which was already available in the test dataset.

Azure ML Step	Function	Dataset
Train Model	Find mathematical relationship(model) between input data and price	Training dataset
Score Model	Predict prices based on the Training model	Testing dataset. Added 1 more column of forecasted price.
Evaluate Model	Calculate the difference between prediction and the actual price	Testing data set.

Score Model

Before going to evaluation, it is pertinent to investigate the output of Score Model and what has been scored.

Understanding Scoring

When we were training our model, we selected the Label column as Price.

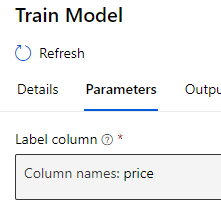
Training model for label price means in simple terms is :

Using 25 other columns in the data, find what is the best combination of values, which can predict the value of our Label column (price)

Scoring model

1. Used training model to predict the value of price
2. Used test dataset and provide a predicted value of price

Therefore, after scoring, we will have an extra column added at the end of the scored data set, called Scored Labels. It looks like this in preview

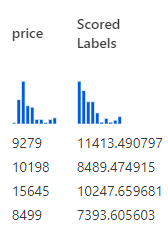
This new column “Scored Labels” is the predicted price. We can use this column to calculate the difference between the actual price which was available in the test data set and how the predicted price (Scored Labels) is

The lower the difference, the better the model is. Hence, we will use the difference as a measure to evaluate the model. There are several metrics which we can use to evaluate the difference.

Evaluate Model

We can investigate these metrics by right clicking on Evaluate Model > Preview data > Evaluation results

The following metrics are reported:

Both Mean Absolute Error and Root Mean Square error are averages of errors between actual values and predicted values.

I will take the first two rows of the scored dataset to explain how these metrics evaluate the model.

make	Wheel-base	length	width	….	Price	Predicted price (Scored Label)
Mitsubishi	96.3	172.4	65.4	…	9279	11413.49
Subaru	97	173.5	65.4	…	10198	8489.47

Absolute Errors

Mean Absolute Error

Evaluates the model by taking the average magnitude of errors in predicted values. A lower value is better

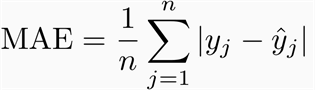
Using the table above, MAE will be calculated as :

Price	Predicted price (Scored Label)	Error = Prediction – Price	Magnitude of error	Average of error
9279	11413.49	2,134.49	2,134.49	854.76
10198	8489.47	-1,708.53	1,708.53

854.76 for the above 2 rows is the average error. Let’s assume there was another model whose MAE will be 500.12. If we were comparing two models

Model 1 : 854.76

Model 2 : 500.12

In this case, model 2 will be more efficient than Model 1 as its average absolute error is less.

Root Mean Squared error

RMSE also measures average magnitude of the error. A lower value is better. However, differs from Mean Absolute Error in two ways :

1. it creates a single value that summarized the error
2. Errors are squared before they are averaged, hence it gives relatively high weight to large errors. E.g., if we had 2 error values of 2 & 10, squaring them would make them 4 and 100 respectively. This means that larger values get disproportionately large weightage.

This means RMSE should be more useful when large errors are particularly undesirable.

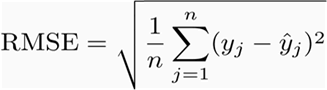
Using the table above, RMSE will be calculated as :

Price	Predicted price (Scored Label)	Error = Prediction – Price	Square of Error	Average of Sq. Error	Square root.
9279	11413.49	2,134.49	4,556,047.56	3,737,561.16
10198	8489.47	-1,708.53	2,919,074.76

Relative Errors

To calculate relative error, we first need to calculate the absolute error. Relative error expresses how large the absolute error is compared with the total object we are measuring.

Relative Error = Absolute Error / Known Value

Relative error is expressed as a fraction, or multiplied by 100 to be expressed as a percent.

Relative Squared error

Relative squared error compares absolute error relative to what it would have been if a simple predictor had been used.

This simple predictor is average of actual values.

Example :

In the Automobile price prediction, we have an absolute error of our model which is Total Squared Error.

Instead of using our model to predict the price, if we just take an average of the “price” column. Then find squared error based on this simple average. It will give us a relative benchmark to evaluate our original error with.

Therefore, the relative square error will be :

Relative Squared Error = Total Squared Error / Total Squared Error of simple predictor

Using the two-row example to calculate RSE :

Calculate Sum of Squared based on Simple Predictor of Average

Price	Average of Price (New Scored Label)	Error = Prediction – Price	Sum of Squared
9279	9,738.5	459.5
10198	9,738.5	459.5

 

Mathematically relative squared error, Ei of an individual model i is evaluated by :

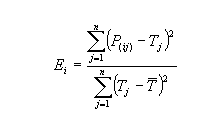
Relative Absolute Error

RAE compares a mean error to errors predicted by a trivial or naïve model. A good forecasting model will produce a ratio close to zero. A poor model will produce a ratio greater than 1.

Relative Absolute Error = Total Absolute Error / Total Absolute Error of simple predictor

Coefficient of determination

The coefficient of determination represents the proportion of variance for a dependent variable (Prediction) that’s explained by an independent variable (attribute used to predict).

In contrast with co-relation which explains the strength of the relationship between independent and dependent variables, the Coefficient of determination explains to what extent variance of one variable explains the variance of the second variable.

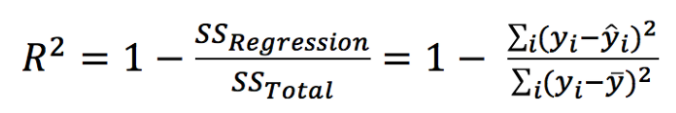
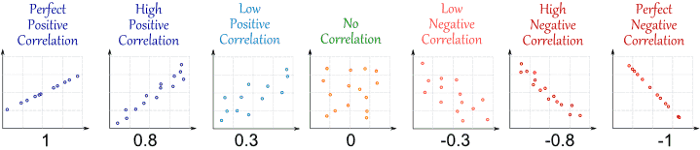
R (Correlation) (source: http://www.mathsisfun.com/data/correlation.html)