A vector in the context of NLP is a multi-dimensional array of numbers that represents linguistic units such as words, characters, sentences, or documents.
Motivation for Vectorisation
Machine learning algorithms require numerical inputs rather than raw text. Therefore, we first convert text into a numerical representation.
Tokens
The most primitive representation of language in NLP is a token. Tokenisation breaks raw text into atomic units – typically words, subwords or characters. These tokens form the basis of all downstream processing. A token is typically assigned a Token ID e.g. “Cat”—> 310 . However, tokens themselves carry no meaning unless they’re transformed into numeric vector.
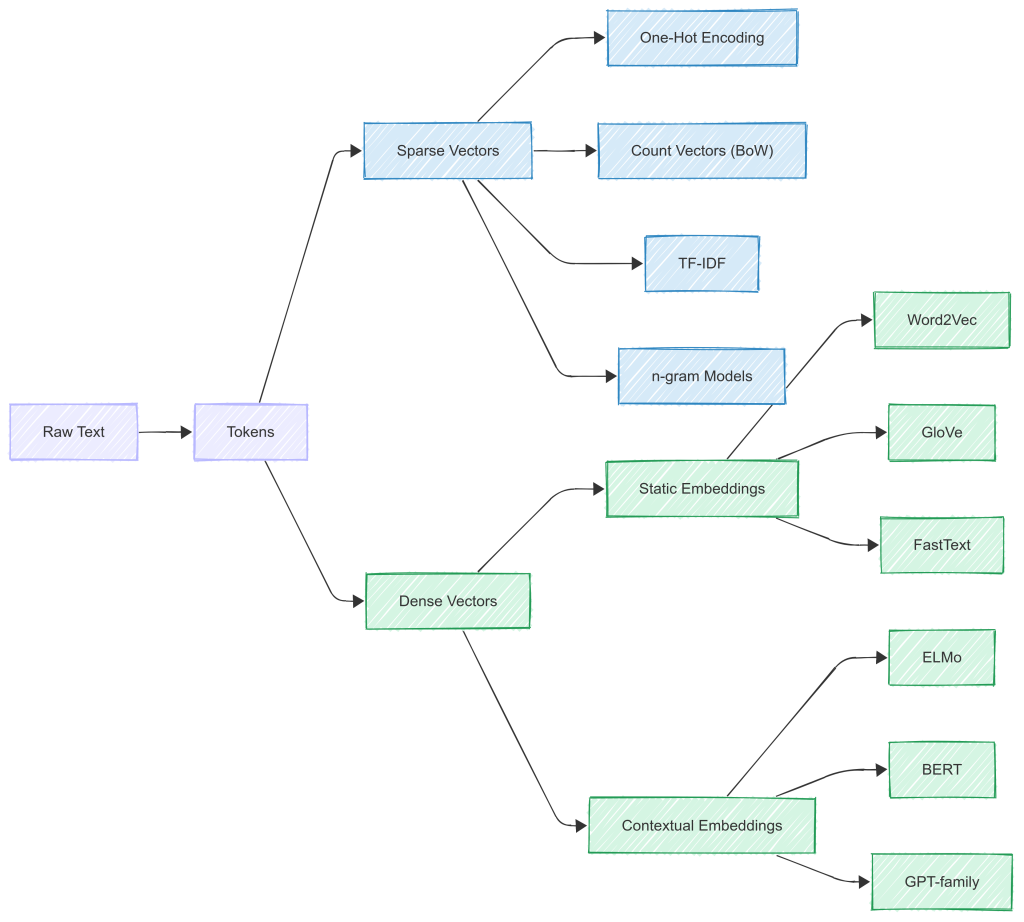
Vectors
Although tokens and token IDs are numeric representations, they lack inherent meaning. To make these numbers meaningful mathematically, they are used as building blocks for vectors.
Vector is a mathematical representation in high-dimensional space. What that means is it carries more context than a bare number itself . As a simplified example , consider “cat”represented in a 5 dimension vector.
"cat" → [0.62, -0.35, 0.12, 0.88, -0.22]
| Dimension | Value | Implied Meaning (not labeled in real models, just illustrative) |
|---|---|---|
| 1 | 0.62 | Animal-relatedness |
| 2 | -0.35 | Wild vs Domestic (negative = domestic) |
| 3 | 0.12 | Size (positive = small) |
| 4 | 0.88 | Closeness to human-associated terms (like "pet", "owner", "feed") |
| 5 | -0.22 | Abstract vs Concrete (negative = more physical/visible) |
Embeddings
If we consider the our example of word "cat", its embedding vector consists of values that are shaped by exposure to language data—such as frequent co-occurrence with words like "meow", "pet", and "kitten". This contextual usage informs how the embedding is constructed, positioning "cat" closer to semantically similar words in the vector space.
More broadly, while vectors provide a numeric way to represent tokens, embeddings are a specialised form of vector that is learned from data to capture linguistic meaning. Unlike sparse or manually defined vectors, embeddings are dense, low-dimensional, and trainable.
| Dimension | Value (Generic Vector) | Value (Embedding) | Implied Meaning (illustrative only) |
|---|---|---|---|
| 1 | 0.62 | 0.10 | Animal-relatedness |
| 2 | -0.35 | 0.05 | Wild vs Domestic |
| 3 | 0.12 | -0.12 | Size |
| 4 | 0.88 | 0.02 | Closeness to human-associated terms (e.g., pet, owner) |
| 5 | -0.22 | -0.05 | Abstract vs Concrete |
Learned Embedding vs Generic Vector for "cat"
Vectorisation Algorithms
Given below is a brief summary of major vectorisation algorithms and their timeline.
Early Algorithms: Sparse Representations
Traditional NLP approaches like Bag of Words (BoW) and TF-IDF relied on token-level frequency information. They represent each document as a high-dimensional vector based on token counts.
Bag of Words (BoW)
- Represents a document by counting how often each token appears.
- Treats all tokens independently; ignores order and meaning.
- Output: sparse vector with many zeros.
TF-IDF (Term Frequency-Inverse Document Frequency)
- Extends BoW by scaling down tokens that appear in many documents.
- Aims to highlight unique or important tokens.
- Output: still sparse and high-dimensional.
These approaches produce sparse vectors. As vocabulary size grows, vectors become inefficient and incapable of generalising across related words like "cat" and "feline."
Transition to Dense Vectors: Embeddings
To overcome the limitations of sparse representations, researchers introduced dense embeddings. These are fixed-size, real-valued vectors that place semantically similar words closer together in the vector space. Unlike count-based vectors, embeddings are learned through training on large corpora.
Early Embedding Algorithms – Dense Representation
Word2Vec (2013, Google – Mikolov)
- Learns dense embeddings using a shallow neural network.
- Words that appear in similar contexts get similar embeddings.
- Two training strategies:
- CBOW (Continuous Bag of Words): Predicts the target word from its surrounding context.
- Skip-Gram: Predicts surrounding words from the target word.
- Efficient training using negative sampling.
- Limitation: Produces static embeddings. A word has one vector regardless of its context.
GloVe (2014, Stanford)
- Stands for Global Vectors.
- Learns embeddings by factorising a global co-occurrence matrix.
- Combines global corpus statistics with local context windows.
- Strength: Captures broader semantic patterns than Word2Vec.
- Limitation: Still produces static embeddings.
Embedding Algorithms – Contextual Embeddings
Even though Word2Vec and GloVe marked a huge advancement, they had a major drawback: they generate one embedding per token, regardless of context. For example, the word "bank" will have the same vector whether it refers to a financial institution or a riverbank.
This limitation led to contextual embeddings such as:
- ELMo (Embeddings from Language Models): Learns context from both directions using RNNs.
- BERT (Bidirectional Encoder Representations from Transformers): Uses transformers to generate context-aware embeddings where each token’s representation changes depending on its surrounding words.
Sparse vs Dense
| Feature | Sparse Vectors (BoW/TF-IDF) | Dense Embeddings (Word2Vec, GloVe) |
|---|---|---|
| Dimensionality | Very high | 100–300 |
| Vector content | Mostly zeros | Fully populated |
| Captures word similarity | No | Yes |
| Context awareness | No | Partially |
| Efficient for learning | No | Yes |
Summary Timeline of Key Algorithms
| Year | Algorithm | Key Idea | Embedding Type |
|---|---|---|---|
| Pre-2010 | BoW, TF-IDF | Token count or frequency | Sparse Vector |
| 2013 | Word2Vec | Predict words using neural networks | Static Embedding |
| 2014 | GloVe | Factorize co-occurrence matrix | Static Embedding |
| 2018 | ELMo | Deep contextual embeddings via language modeling | Contextual Embedding |
| 2018 | BERT | Transformer-based contextual learning | Contextual Embedding |
